How to Calculate the Slope on a Topographic Map using Contour Lines

Use Equator to Determine the Slope or Gradient on a Contour Map

By studying topographic maps, we can gain invaluable insight into the Earth’s terrain and better understand the complex landscapes that shape our environment. The analysis of contour lines on these maps allows us to determine the slope or gradient of each topographical feature, which is important for so many different applications.

In this article, learn what slope is when referring to topography and why it is important, how to calculate the slope, and how to use Equator to find the slope.

When studying topography, slope refers to the steepness or gradient of the terrain. It describes how quickly the elevation changes over a horizontal distance, and can be referred to as gradient, grade, incline, or pitch. The easiest way to explain slope is to pretend you are standing at the bottom of a hill. The incline of that hill is the slope.

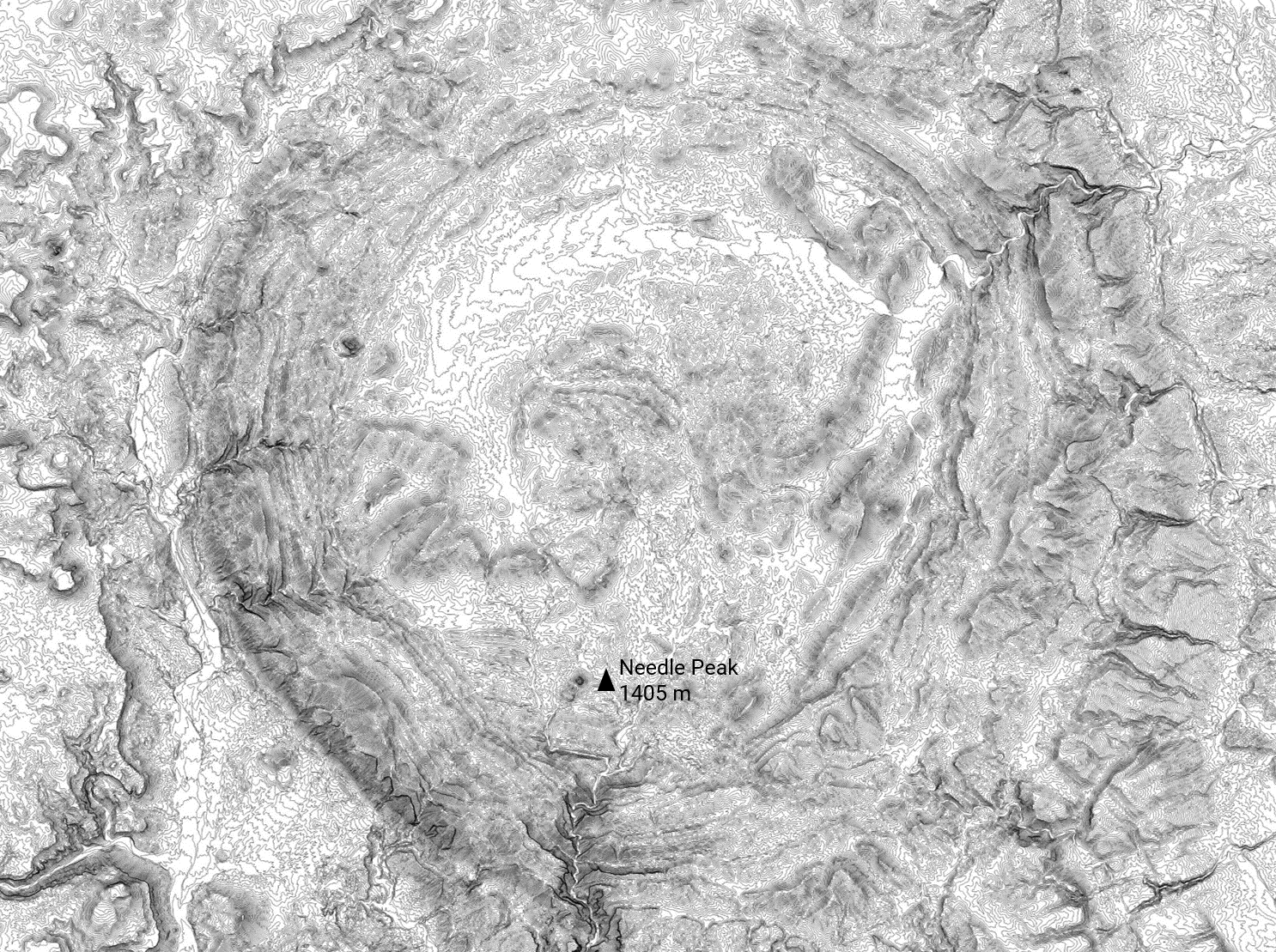
A terrain with contour lines that are widely distributed indicates a gradual slope. A narrow distance between the contour lines indicates a steep slope. Circular contour lines indicate the presence of a hill or a depression.

coastal erosion

Determining the slope is important for a wide range of applications. In environmental analysis, calculating slope can help determine the amount of erosion expected during a rainstorm, identify areas that are prone to landslides, and help identify hydrological patterns which help with conservation efforts and disaster preparedness. In engineering and construction, determining slope is important when designing drainage systems, safe roads and transit systems, and determining when retaining walls are required. In hiking, mountain biking, or mountaineering, determining the slope allows outdoor enthusiasts to choose the most suitable paths given their fitness level, available time, and desired challenge level.

Calculating the slope on a topographic map is similar to calculating the slope of a line on a graph (rise/run). When we look at contour lines, the rise is the difference in elevation between two contour lines. The run is the horizontal distance between those same two contour lines.

To calculate the slope on a topographic map, select two contour lines that you want to calculate the slope between. Determine the vertical distance by identifying the elevation values for each contour line you have selected. Then measure the horizontal distance between these two contour lines by using a ruler. We want to make sure the measurement is in the same unit as the elevation distance. We now have enough information to calculate the slope. Use the following formula:

Slope = change in elevation between two points / horizontal distance between those same two points

We can also calculate the percent slope by multiplying the slope ratio (determined above) by 100.

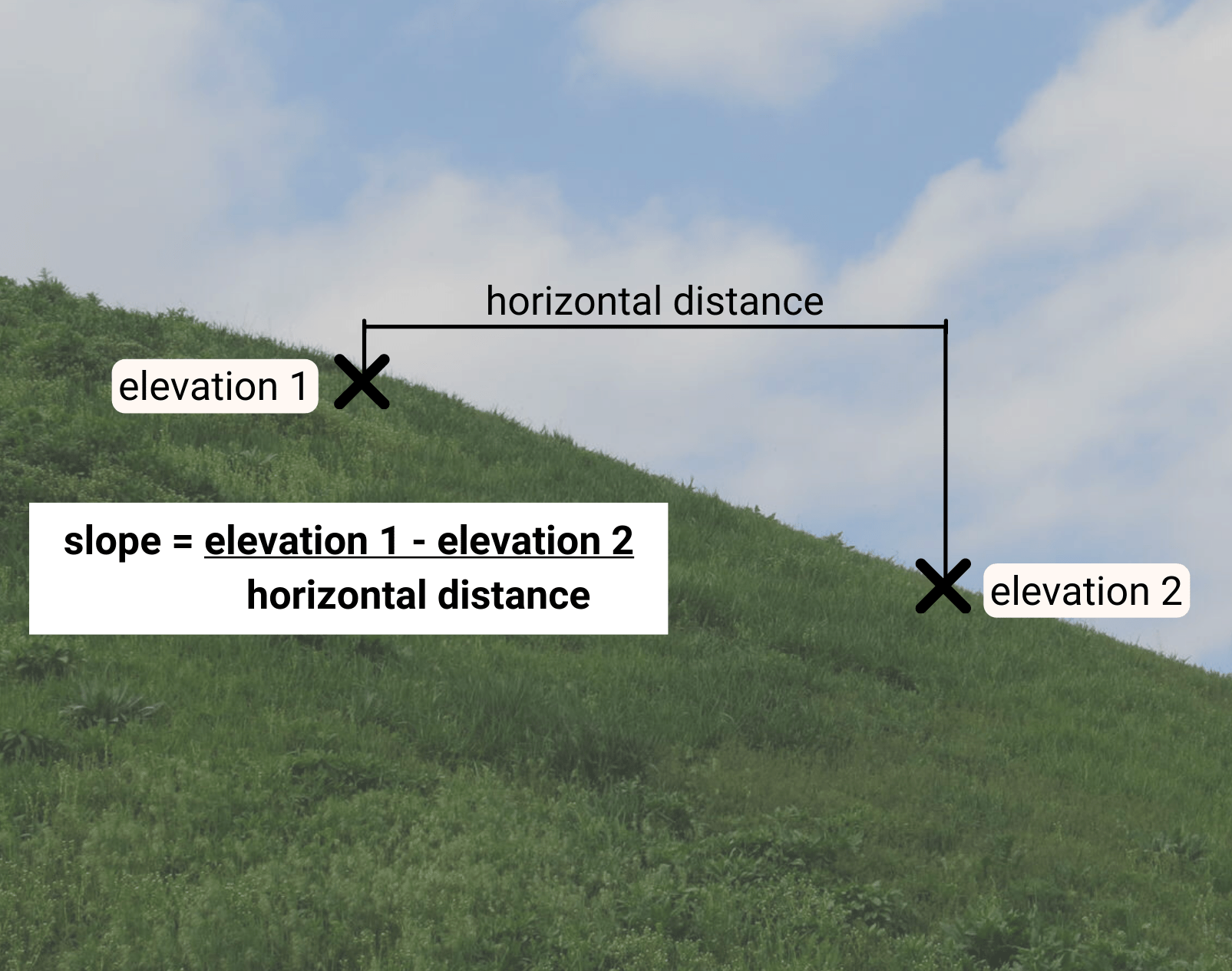
How to calculate the slope of a hill

It is easy to calculate the slope in Equator. Simply follow the few steps below:

1. Login or create an account
2. Select +NEW SITE to create a site around the area you want to calculate the slope
3. Add contours to the map by going to the Data menu and selecting Contours as SHP.
4. Use spot elevation (on the right menu) and apply to two different contour lines on the map to determine the elevation
5. Use the measuring tool (on the right menu) to identify the horizontal distance between the two points by drawing a line perpendicular to the contour lines
6. Calculate the gradient manually by using the formula in the section above (elevation distance/horizontal distance)

Calculating slope in Equator using the spot elevation and measuring tools

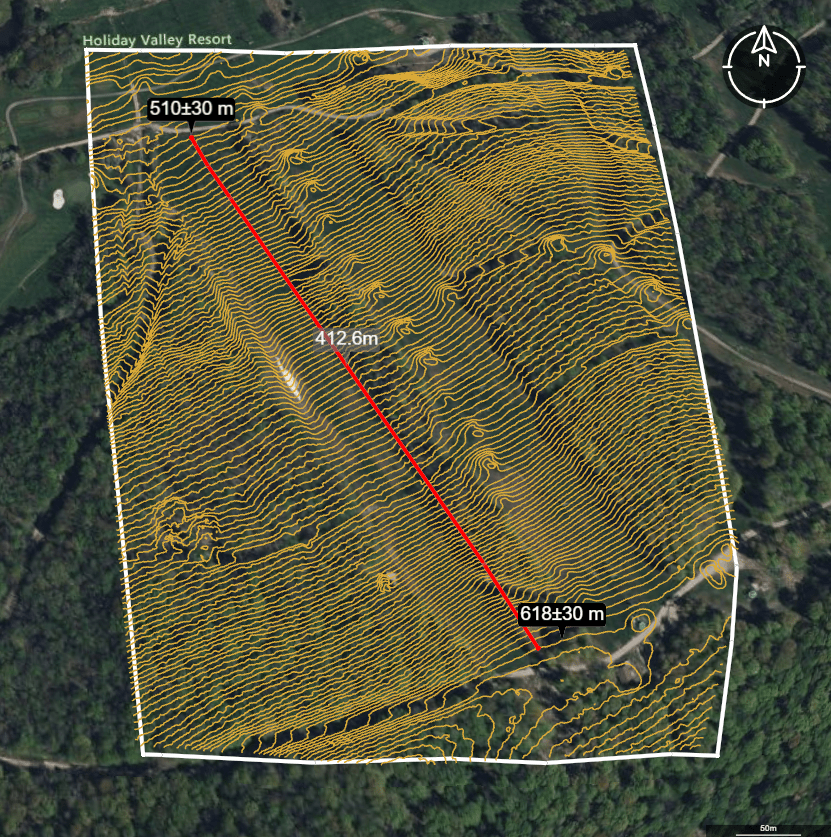
In this Holiday Valley example done in Equator, we can calculate the slope as follows:

Slope = (618.3m – 510.3m) / 412.6m
Slope = 0.26

Slope % = 0.26 x 100
Slope % = 26%